中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード・印刷 根号を含む複雑な式は、なるべく簡単な形に変形してから値を代入し、分配法則や乗法公式を使って√を含む式を計算する練習問題プリントです。展開(乗法公式2) 次の式を計算しなさい (x 1 2)(x 3 2) (x 5 4)(x1 4) (x2y)(x3y) (2x5)(2x6) (3x1)(3x2) (5x2)(5x3) 次の式を計算しなさい (x 3 2) 2 (x5 2) 2 (2x1) 2 (3x2) 2 (xy) 2 (ab) 2 次の式を計算しなさい (xy)(xy) (3x2)(3x2) (1 2 x 1 3 y)(1 2 x1 3 y) (x 4 7)(x4 7) (6x5y)(6x5y) (10x9a)(10x9a) そこで、ここでは乗法公式を楽に暗記するための覚え方を紹介します。 \((xa)(xb) = x^2(ab)xab\)を覚える まずは、この4つの公式の中でももっとも基本の公式である、 $$(xa)(xb) = x^2(ab)xab$$ の覚え方から説明していきます。 まず、\((xa)(xb)\)を展開(計算)すると、3つ項が出てくることを覚えましょう。 例えば、実際の計算の例を出すと、

乗法公式 式の展開公式 19個まとめ 高校数学の美しい物語
乗法公式 展開公式
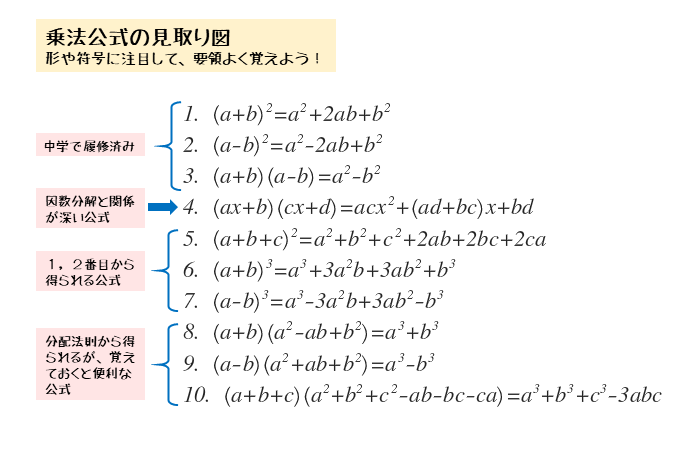
乗法公式 展開公式- 乗法公式は展開公式とも呼ばれます。高校数学の最初のテーマです。 → 乗法公式(式の展開公式)19個まとめ 対称式を素早く正確に展開する3つのコツ 難関大学の入試問題や数学オリンピックの不等式証明問題では複雑な対称式を計算しなければならない問題が出題されます。 → 対称式を基本的な乗法公式(展開公式) I (ab)2=a22abb2 II (a−b)2=a2−2abb2 III (ab) (a−b)=a2−b2



3 8第1章多項式 乗法公式 いろいろな式の展開 中学生
3乗の展開公式は、ちょっと複雑に見えてしまうので苦手な人が多いです。 ですが、やっていることは至ってシンプル! 3乗フォーメーションである 3⇒321⇒312⇒3 これをしっかりと覚えておけば大丈夫ですね(^^) あとは何度も計算練習をして、ミスなくスラスラ解けるようにしておきましょう 展開の4つの基本公式 展開についての,基本的な4つの公式を書きます. これらは,左辺を実際に展開すれば導くことができるので,一度は自分で計算してみてください. さて,4つの公式があるとはいえ, ひとまずは一番上の公式 を使えるようになり2 乗法公式を使って、式を展開できる。 技能 3 式の一部を1つの文字に置き換えて乗法公式の形で 考えることができた。 見・考 4 今回の学習を理解することができた。 関・意 これまでに学んだ公式をまとめると,次のようになる。下の乗法公式をノートに
式の展開公式 こちらの乗法公式は、かっこ内に同じ項が含まれている場合に使うことができます。 使い方は単純! 足したものを真ん中、掛けたものを右に持ってくればOKです。 これは例題を見ながら確認したほうが理解しやすいので、実際に問題を使っ 展開、乗法公式 2 131 0 このノートについて ユリ 展開 乗法公式 数学 3年 math このノートが参考になったら、著者をフォローをしませんか?気軽に新しいノートをチェックすることができます! 著者をフォローする コメント コメントはまだありません。 アプリなら ランキングからも公式を使わず展開したい! ハートの公式!? なんじゃそりゃ! そんなふざけたもん使わずにオレは硬派に問題を解きたいんじゃ! そんなあなたへ ハートの公式を使わずに展開する方法も紹介しておきます。 $$(abc)^2$$ やっぱりかっこの中に3つも項があるとややこしいです。 ということで
しかし、 展開してみると最高次数が3 となります。ですから3次式として扱います。ここでは、このような3次式の展開について学習します。 3次式の展開 3次式の展開では、数学1で学習した 指数法則 や 乗法公式 を利用します。すでに学習した乗法公式を展開(乗法公式1) 次の式を計算しなさい (x1)(x2) (x3)(x5) (x4)(x6) (x7)(x1) (x4)(x7) (x2)(x8) 次の式を計算しなさい (x1) 2 (a5) 2 (x10) 2 (x2) 2 (x3) 2 (x4) 2 次の式を計算しなさい (x1)(x1) (x11)(x11) (x7)(x7) (x8)(x8) 以前、基本展開の公式で二次式の展開について見ました。ここでは、三次式の場合では、式の展開がどうなるかを見ていきます。 三次式の展開 今までに、 $(xy)^2=x^22xyy^2$ などの「2乗の展開」は計算し



中3数学 式の展開 乗法公式を使う展開の4つのポイント たけのこ塾 勉強が苦手な中学生のやる気をのばす




積分定数 超算数 は 展開 は私はわからなかった 正解は 乗法 乗法公式 という用語を覚える必要は全くない というのみならず 乗法公式 が特定の4つの式を指すというのも 闇が深い 画像は 数学中学3年教科書 学校図書 平成27年2月
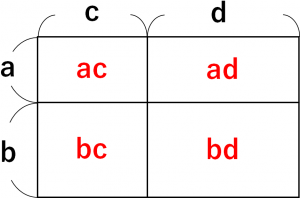
乗法公式を用いた式の展開 乗法公式 \\begin{array}{l} (a \pm b)^2 = a^2 \pm 2ab b^2 \\ (a b)(a b) = a^2 b^2 \\ (x a)(x b) = x^2 (a b)x ab \\ (ax b)(cx d) = acx^2 (ad bc)x bd \\ (a \pm b)^3 = a^3 \pm 3a^2b 3ab^2 \pm b^3 \\ (a \pm b)(a^2 \mp abここで乗法公式について教えてくれるのは湯浅弘一先生(ゆあさま)です。 (3x-5) 2 を展開するには、(a-b) 2 =a 2 -2ab+b 2 の公式を使いましょう。 a=3x,b=5と考えればよいですね。 (3x-5) 2 =(3x) 2 x 2多項式 例題 多項式と単項式の乗法除法 式の展開 乗法公式(xa)(xb)の展開 乗法公式 2乗の展開 乗法公式 和と差の積の展開 式の展開 いろいろな計算 式の展開 四則 因数分解1_共通因数をくくりだす 因数分解2_(xa)(xb) 因数分解3_2乗 因数分解4_(xa)(xa) 因数分解 おきかえ 共通因数をくくりだした後



中三数学 多項式の乗法公式についてなんですが この例1の説明の意味が理解出来ま Yahoo 知恵袋



乗法公式
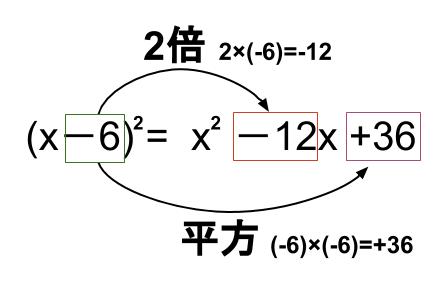
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru中3 乗法公式 2乗の展開 (x5)2 = x22×5×x52 = x210x25 (x4)2 = x22×4×x42 = x28x16 (2x3)2 = (2x)22×3×2x32 っていう展開の式があったとする。 公式つかえば、 (x3)(x3) = x^2 – 3^2 = x^2 – 9 になるね! まとめ:乗法公式をつかえば3秒で展開できる!! 乗法公式はおぼえられそうかな?? ぶっちゃけると、 数学の公式をおぼえるためには語呂とかよりも、




中三受験講座 英数ポイント解説映像授業 進研ゼミ中学講座会員サイト




Math 超速まとめ 式の展開 乗法公式 働きアリ
乗法公式とは 式を展開するときに、次の公式がよく用いられます。 ①: (a+b)²=a²+2ab+b² ②: (a-b)²=a²-2ab+b² ③: (a+b) (a-b)=a²-b² ④: (x+a) (x+b)=x²+ (a+b)x+ab ⑤: (ax+b) (cx+d)=acx²+ (ad+bc)x+bd これらの公式乗法公式とよばれる公式です、 後の 因数分解 という単元でとても大切になるので、必ず覚える ようにしましょう。 覚えるため 式の展開乗法公式を使った文字の置き換え問題の解き方とは? 19年6月14日 suugakubisuketto 中学数学をはじめから分かりやすく COMMENT コメントをキャンセル メールアドレスが公開されることはありません。 * が付いている欄は必須項目です 次回のコメントで使用するためブラウザーに自分例題9 次の式を展開せよ。 d e d e d e f 展開の工夫計算順序 例題 楽な順で乗法を行う。 >例@ 例題 次の式を展開せよ。 d e d e 数学Ⅰ 演習プリント > 乗法公式@ > 展開の工夫 その1@ 年 組 番( )



4月22日更新 中3一斉授業 数学 展開 乗法公式 担当 中嶋 成績 上がってます 根城学習塾 八戸市




Youtube解説 中3数学 式の展開 乗法公式 コジ塾チャンネル コジ塾
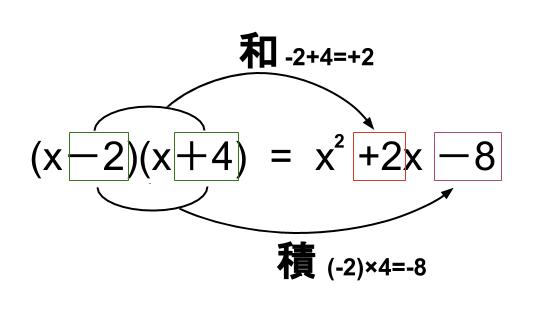
多項式の展開の公式 \((xa)(xb)=x^{2}(ab)xab\) \((xa)^{2}=x^{2}2axa^{2}\) \((xa)^{2}=x^{2}2axa^{2}\) \((xa)(xa)=x^{2}a^{2}\) 係数が2以上の変数をもつ多項式同士に公式を用いた展開方法 例1\((3x4)(3x1)\)を展開してみよう乗法公式を用いた式の展開,式の展開について,基本的パタンをまとめたものを乗法公式という。(xa)(xb)=x^2(ab)xab (xa)(xb)=x^2(ab)xab 乗法公式 (xa)(xb)の展開基本的な乗法公式(展開公式) i あなたの目の動きをたどってみると,3乗の展開公式のところを何度も見ています.確かに公式vi~ixがあなたの弱い箇所なのでそこをもう一度よく読んでみるとよいでしょう. 個別の頁からの質問に対する回答展開公式1について/ viiiix
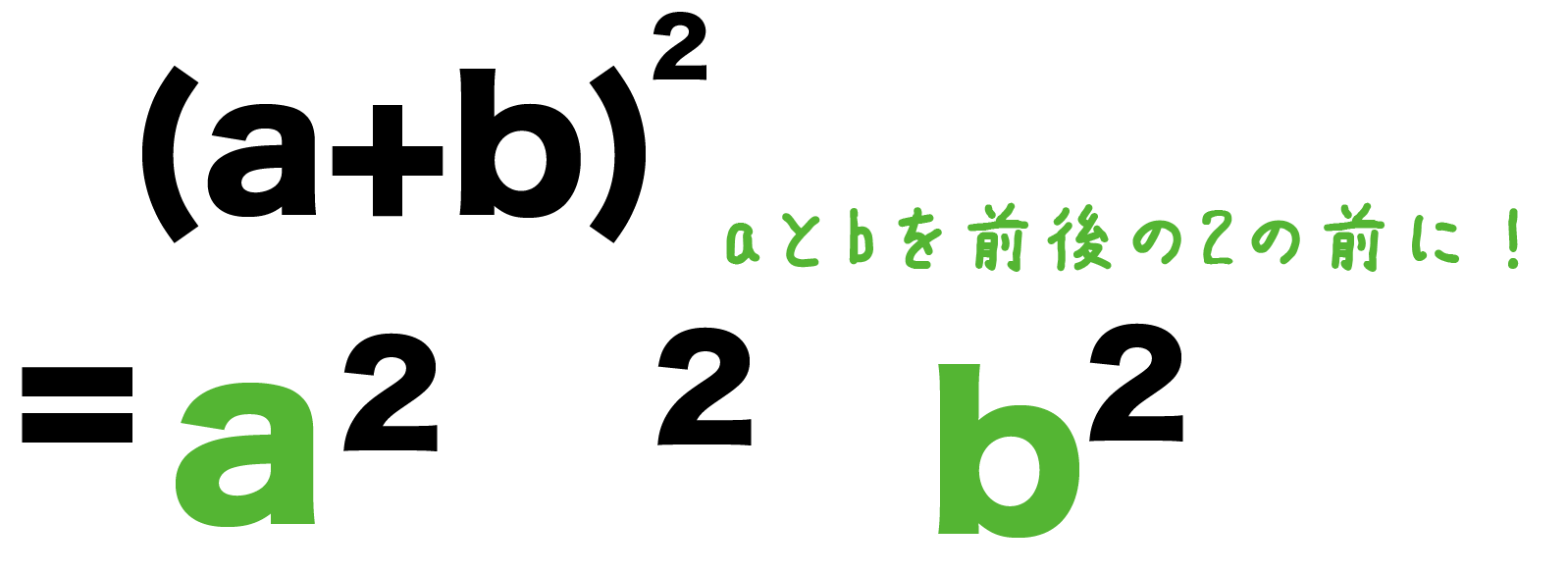



式の展開 乗法公式を1瞬でマスターできる3つの覚え方 Qikeru 学びを楽しくわかりやすく




高校数学 数 7 展開 3次式の公式編 Youtube
4乗の展開公式 ( a b) 4 = a 4 4 a 3 b 6 a 2 b 2 4 a b 3 b 4 (ab)^4=a^44a^3b6a^2b^24ab^3b^4 (a b)4 = a4 4a3b 6a2b2 4ab3 b4 ( a − b) 4 = a 4 − 4 a 3 b 6 a 2 b 2 − 4 a b 3 b 4 (ab)^4=a^44a^3b6a^2b^24ab^3b^4 (a− b)4 = a4 −4a3b 6a2b2 −4ab3 b4乗法公式や因数分解を利用した数値計算問題の解き方です。 中学3年で覚えることになる展開公式や因数分解は暗記するためにあるのではありません。 いろいろな計算を楽にするためにあるので利用方法を解説しておきます。 基本問題しか 中学数学の乗法公式(展開公式) \((xa)(xb)=x^2(ab)xab\) \((xa)^2=x^22axa^2\) \((xa)^2=x^22axa^2\) \((xa)(xa)=x^2a^2\) \((axb)(cxd)=acx^2(adbc)xbd\) 高校数学の乗法公式(展開公式) \((xa)^3=x^33x^2a3xa^2a^3\) \((xa)^3=x^33x^2a3xa^2a^3\)



中学3年の数学 乗法の公式について 栄翔塾




乗法公式 多項式の展開公式 の覚え方と使い方 数学fun
高校までに習う、基本的な乗法公式の内容とは? 乗法公式というのは、さまざまな式の展開に対応した公式です。 ここでは高校までに扱う乗法公式のうち、基本的な10のパターンを紹介します。複雑な式の展開が早く進められるようになるので、覚えておいてください。 ①(xa)(xb)=x 2 (ab)xab ②(ab)(ab)=a 2b 2①例: ( )の2乗のパターン。この場合は、 「2乗+2 +2乗」という感覚です!!3乗の展開公式はすべての項に3が入っています。 初めと終わりの項が3乗されるのは覚えやすいと思います。 覚えづらいのが中央の2項です。 中央の2項に関しては、2乗1乗・1乗2乗となるように掛け合わせたものを3倍すれば展開は終了です。



3



中3数学12 式の計算2 乗法 公式1 基本問題プリント 問題 302




中3数学 展開 乗法の公式 の定期テスト過去問分析問題 Atstudier




中3数学 乗法公式 応用 置き換え 1 Youtube



乗法公式




中3 数学 式の展開4 乗法公式1 10分 Youtube




乗法公式の問題 a b a b の展開を練習しよう 中学や高校の数学の計算問題



中学数学 式の展開 乗法公式 中学数学の無料オンライン学習サイトchu Su




乗法公式 式の展開公式 19個まとめ 高校数学の美しい物語




式の展開 乗法公式の利用2 ドリるーむ



3
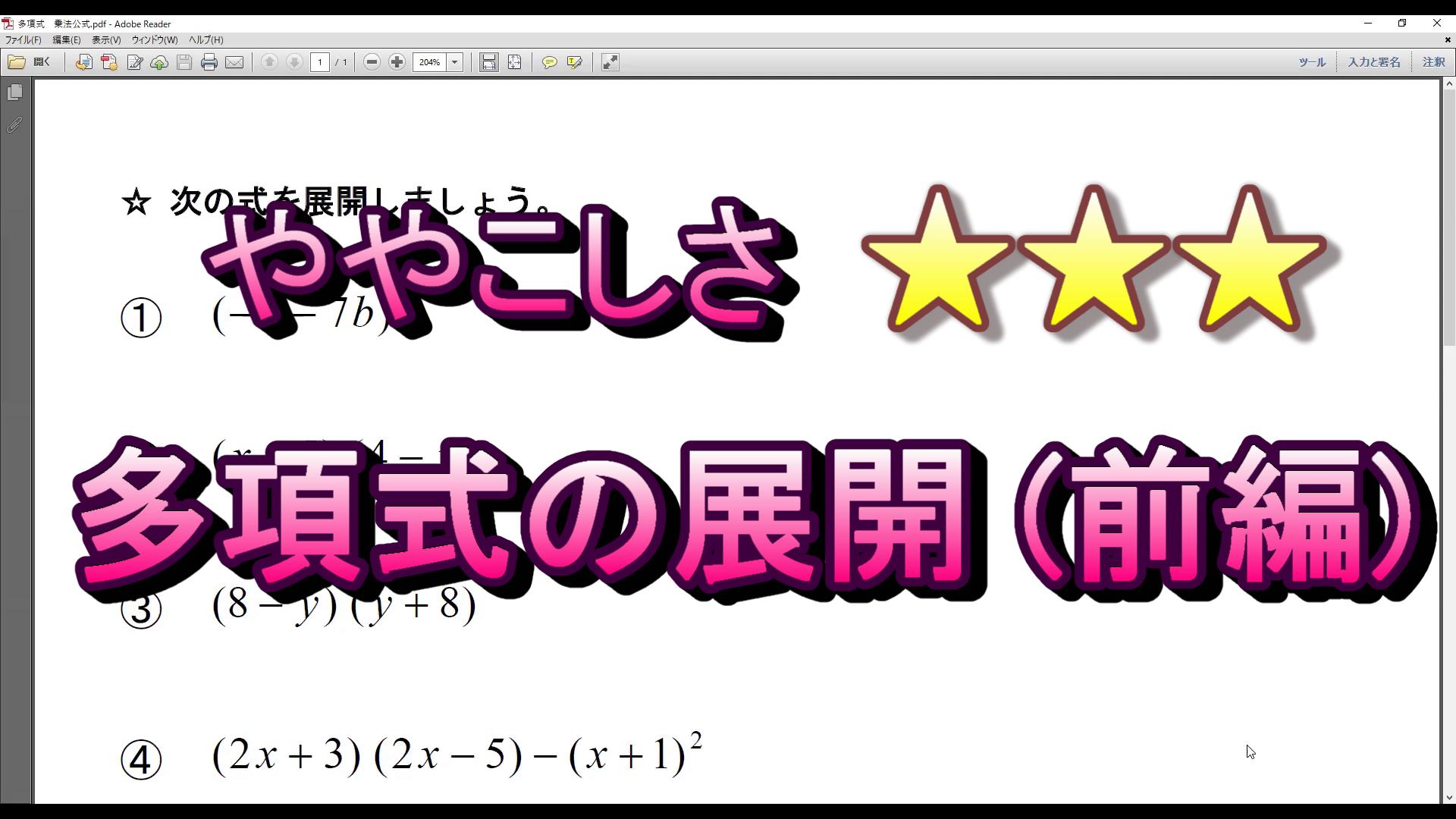



いろいろな多項式を展開してみよう 前編 インターネット家庭教師のアスミラ




高校数学 展開の工夫 共通部分の置き換え 受験の月



乗法公式とは 1分でわかる意味 公式の覚え方 問題 因数分解との関係




中学数学3年 展開と乗法公式 受験の月




多項式の乗法公式を理解しよう 数学嫌いな子のための簡単理解法 分かりにくいを分かりやすいに



Studydoctor3項式の展開 中3数学 Studydoctor
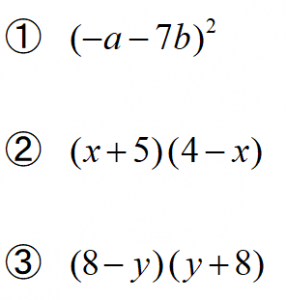



いろいろな多項式を展開してみよう 前編 インターネット家庭教師のアスミラ



U9j580gf8iba369ji2w Xyz P 565




乗法公式の利用 いろいろな式の展開 前半 教遊者
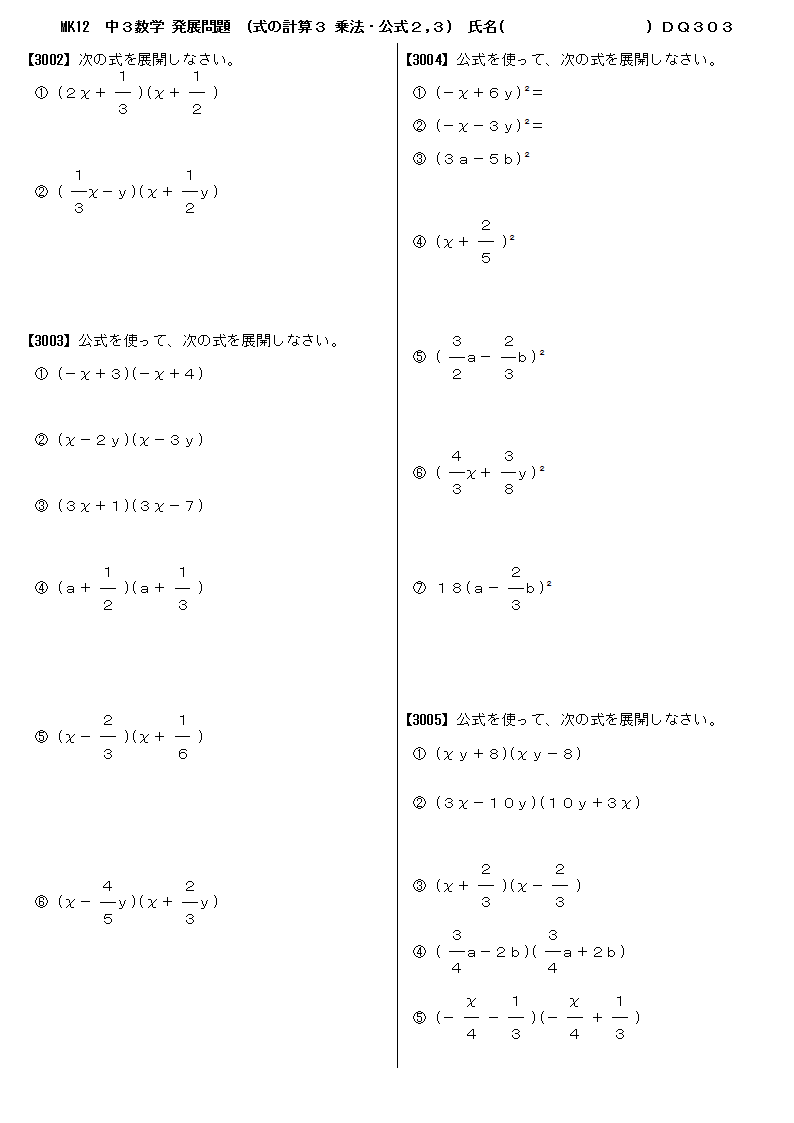



無料 中3数学 発展 応用問題 問題プリント 303 式の計算3 乗法 公式2 3




乗法公式 多項式の展開公式 の覚え方と使い方 数学fun




ม 3 โน ตของ 数学 3年 乗法公式の展開と計算 ช น Junior Clear




三乗の公式 展開と因数分解 高校生向け受験応援メディア 受験のミカタ




中学数学 多項式の計算 ママ塾ノート



展開公式



3 8第1章多項式 乗法公式 いろいろな式の展開 中学生




乗法公式による式の展開と因数分解 中学数学の多項式計算 リョースケ大学




中学数学 攻略 乗法公式と展開 数樂管理人のブログ




多項式の乗法の公式 数学i フリー教材開発コミュニティ Ftext



Ten Tokyo Shoseki Co Jp Text Hs Gk Digi Book Sugaku Dmeister Sample Data 2 318 2 Standard 318 2 Kyoukashoword 318 2 Kyoukashoword 1 1 Pdf




至急お願い致します 中3 式の計算 乗法公式 式の展開 Clear



数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん




乗法公式の覚え方 4つの乗法公式を簡単に覚える方法 数学の面白いこと 役に立つことをまとめたサイト



展開公式



乗法公式
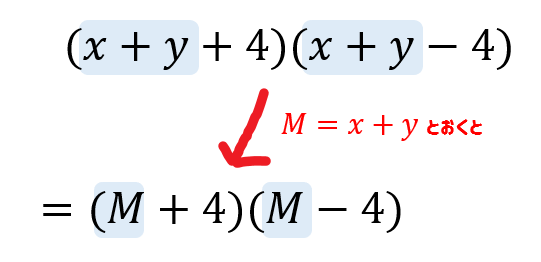



高校数学 式の展開の工夫 置き換えや組み合わせを利用するやり方を解説 数スタ



中3数学 基本問題 問題 303 式の計算3 乗法 公式2 3 プリント




中3数学 平方根 29 中学数学高校数学個別指導in山形市 数専ゼミ




式の展開 中3のいろいろな展開問題 乗法公式を使いこなそう 中学数学をはじめから分かりやすく




式の展開 乗法公式を1瞬でマスターできる3つの覚え方 Qikeru 学びを楽しくわかりやすく




式の展開 乗法公式を1瞬でマスターできる3つの覚え方 Qikeru 学びを楽しくわかりやすく




中3数学 展開の公式のやり方は 問題を使って徹底解説 数スタ




中学数学 多項式 の教え方 乗法公式




中3の皆さん 乗法公式マスターしましたか 勉強方法




三乗の公式 展開と因数分解 高校生向け受験応援メディア 受験のミカタ




3乗の因数分解 展開 公式 理系ラボ
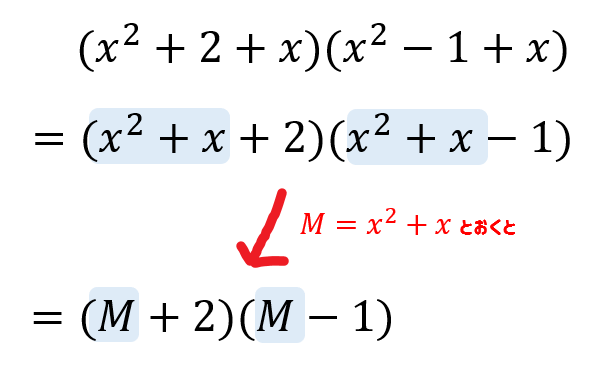



高校数学 式の展開の工夫 置き換えや組み合わせを利用するやり方を解説 数スタ




板書ノート公開 中3数学 式の展開 後藤塾ブログ



2



乗法公式




式と証明 3次式の展開について 日々是鍛錬 ひびこれたんれん




乗法公式による式の展開と因数分解 中学数学の多項式計算 リョースケ大学



中学数学 式の展開 乗法公式 中学数学の無料オンライン学習サイトchu Su




乗法公式 式の展開の解き方 授業動画つきで簡単に理解が出来る



数学iの数と式の乗法公式に関して質問です 画像の公式の右辺の Yahoo 知恵袋
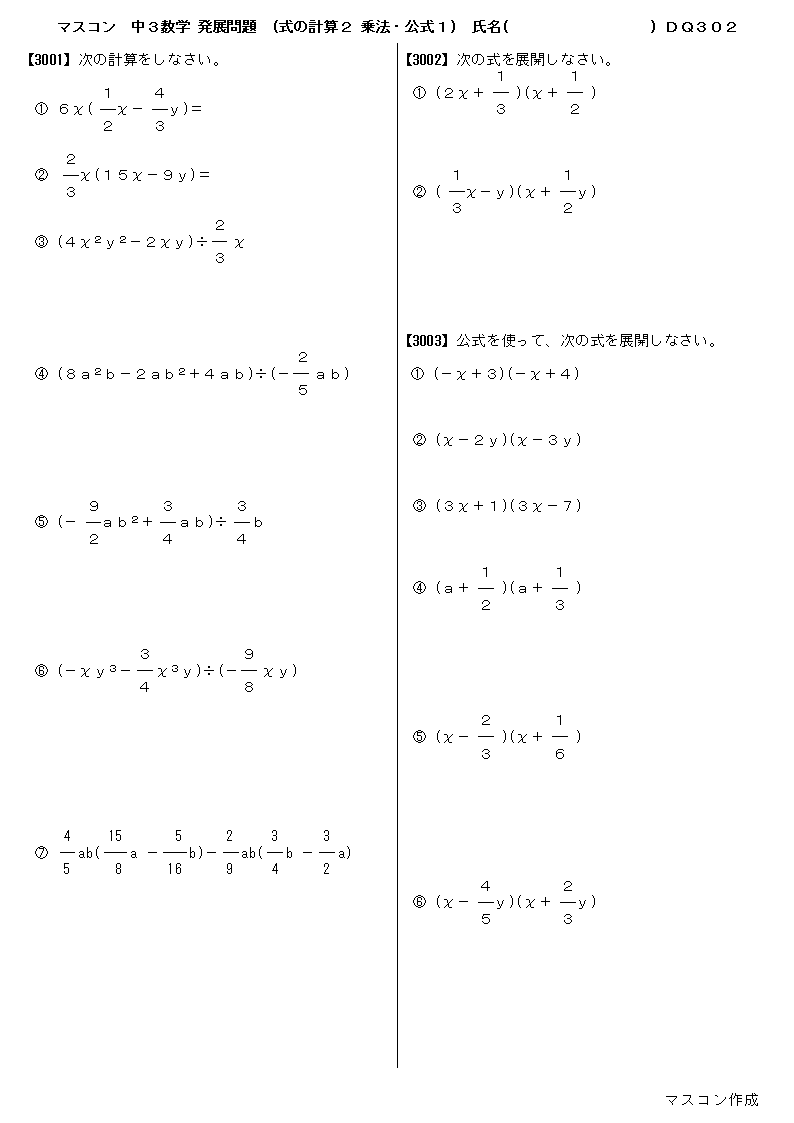



中3数学の発展問題プリント 問題と解答
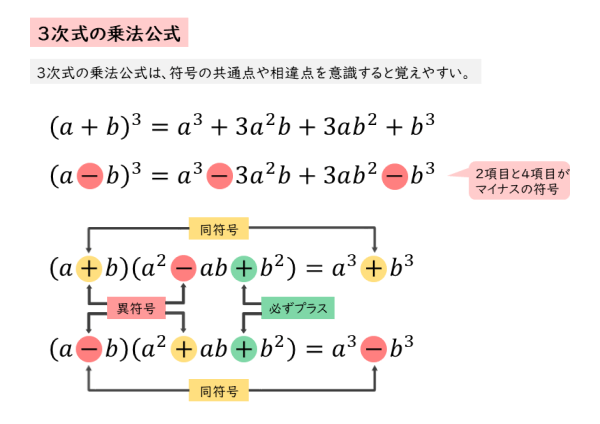



式と証明 3次式の展開について 日々是鍛錬 ひびこれたんれん



Sukinakazu Net Takousiki Takousiki Pdf




乗法公式による式の展開と因数分解 中学数学の多項式計算 リョースケ大学




式の展開 乗法公式を1瞬でマスターできる3つの覚え方 Qikeru 学びを楽しくわかりやすく



中学校3年生の数学の授業




中3 展開と因数分解5 乗法の公式 予習 中学数学の勉強に




乗法公式 多項式の展開公式 の覚え方と使い方 数学fun




中学数学 多項式 の教え方 乗法公式



3 7第1章多項式 乗法公式 いろいろな式の展開




乗法公式 無料で使える中学学習プリント



1




乗法公式 X A X B の展開




乗法公式の覚え方 4つの乗法公式を簡単に覚える方法 数学の面白いこと 役に立つことをまとめたサイト




乗法公式 多項式の展開公式 の覚え方と使い方 数学fun




乗法公式による式の展開 効率良い復習 テクニックで勉強 テストが楽しくなるブログ




乗法公式の利用 いろいろな式の展開 前半 教遊者
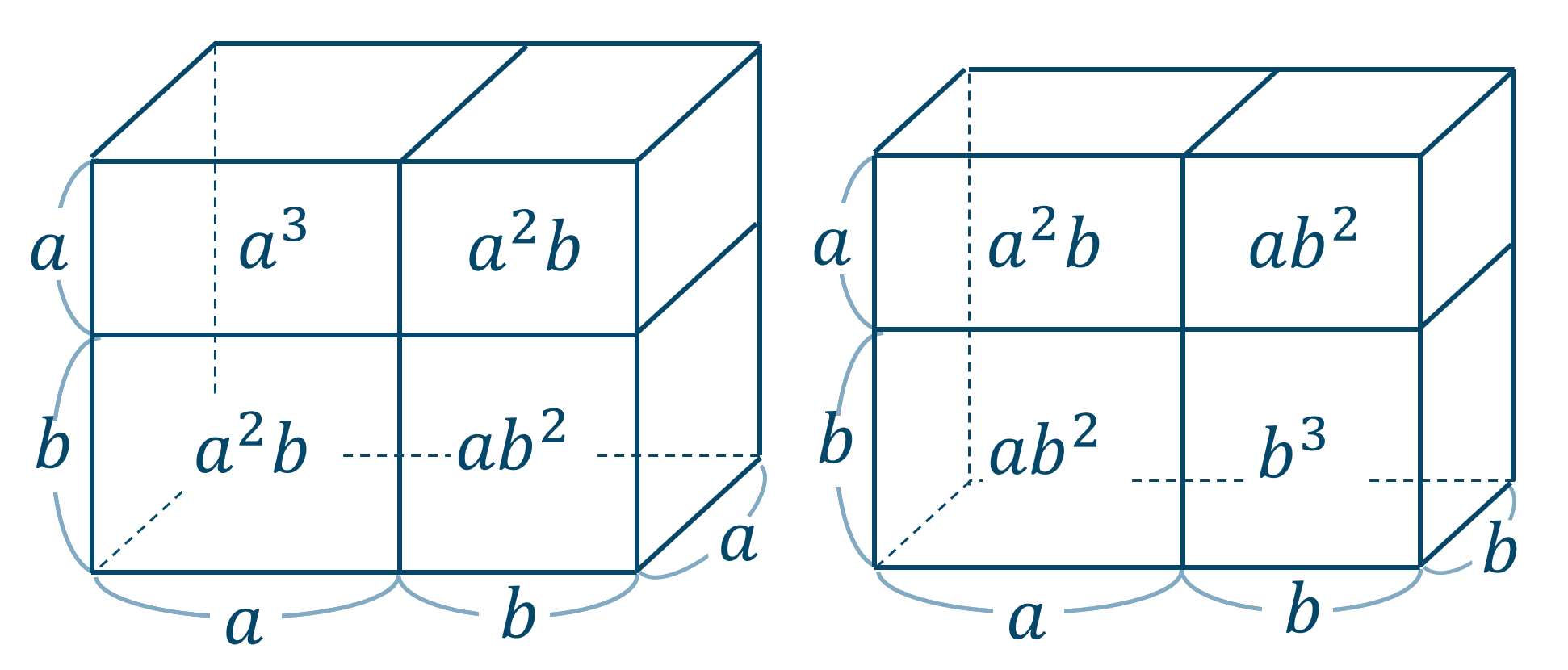



数学 3次式の展開公式の使い方とコツ ページ 2 教科書より詳しい高校数学



展開公式とは 1分でわかる意味 二乗 3乗の公式 覚え方 問題



Math 超速まとめ 式の展開 乗法公式 働きアリ The 2nd




モノマナビ研究所




式の展開 中3のいろいろな展開問題 乗法公式を使いこなそう 中学数学をはじめから分かりやすく



乗法公式 時習館 ゼミナール 高等部



塾長の備忘録 数学 乗法公式の整理




中3数学の計算問題プリント 式の展開 と因数分解 桜花 現役バイト塾講師 Note




数学 2次式の展開のコツと乗法公式 展開公式 教科書より詳しい高校数学




Tossランド コロナ対応 乗法公式による展開




式の展開 中3のいろいろな展開問題 乗法公式を使いこなそう 中学数学をはじめから分かりやすく




中3 数学 乗法公式 1 無料学習プリント教材




中3 数学 乗法公式 まとめ 中学生 数学のノート Clear



乗法公式とは 1分でわかる意味 公式の覚え方 問題 因数分解との関係




乗法公式 無料で使える中学学習プリント




乗法公式は覚えなくてもいいんじゃないだろうか 学習塾q




数と式 整式の展開と乗法公式について 日々是鍛錬 ひびこれたんれん



数学 中3 3 展開 4つの公式 Youtube



1



0 件のコメント:
コメントを投稿